Skip to contents

Internals

Source: vignettes/articles/internals_pipeop_torch.Rmd
internals_pipeop_torch.Rmd

This vignette contains technical details about the inner workings of representing neural networks as mlr3pipelines::Graphs. If you are not familiar with mlr3pipelines, start by reading the related sections from the mlr3 book first.

A torch Primer

We start by sampling some input tensor: 2 batches with 3 features:

input = torch_randn(2, 3)
input
#> torch_tensor
#>  0.4996 -0.4595  1.4343
#>  1.0477  0.1371  0.4999
#> [ CPUFloatType{2,3} ]

A nn_module is constructed from a nn_module_generator. nn_linear is one of the simpler generators:

module_1 = nn_linear(in_features = 3, out_features = 4, bias = TRUE)

Applying this module gives a 2-batch of 4 units:

output = module_1(input)
output
#> torch_tensor
#>  0.1785 -0.0593 -0.4577 -0.5281
#>  0.7633  0.1062 -0.4100 -0.7551
#> [ CPUFloatType{2,4} ][ grad_fn = <AddmmBackward0> ]

A neural network with one (4-unit) hidden layer and two outputs needs the following ingredients

activation = nn_sigmoid()
module_2 = nn_linear(4, 3, bias = TRUE)
softmax = nn_softmax(2)

We can pipe a tensor through the layers as follows.

output = module_1(input)
output = activation(output)
output = module_2(output)
output = softmax(output)
output
#> torch_tensor
#>  0.2276  0.3846  0.3878
#>  0.2154  0.3835  0.4011
#> [ CPUFloatType{2,3} ][ grad_fn = <SoftmaxBackward0> ]

We will now continue with showing how such a neural network can be represented in mlr3torch.

Neural Networks as Graphs

In mlr3torch, nn_modules are wrapped in a PipeOpModule. This has the advantage that the network structure can be represented as an mlr3pipelines::Graph object where it is made explicit (can be plotted, can be extended or manipulated), compared to e.g. writing a function that pipes input through a series of modules.

A PipeOpModule can be used to wrap a module directly, but it is usually constructed by a PipeOpTorch (see later). It typically has a single input and a single output, although multiple inputs are possible (module is then called with multiple arguments), and multiple outputs are possible when the module-function returns a list. The input and output channels must be explicitly declared then during construction. We will now continue to recreate the above network using PipeOpModules.

We can wrap the linear module_1 layers like this:

library(mlr3torch)
po_module_1 = po("module_1", module = module_1)

Note that po("module_1") is equivalent to po("module", id = "module_1"). This mechanism is convenient to avoid ID clashes in graphs that contain the same PipeOp multiple times.

We can use the generated PipeOp in the familiar way:

output = po_module_1$train(list(input))[[1]]
output
#> torch_tensor
#>  0.1785 -0.0593 -0.4577 -0.5281
#>  0.7633  0.1062 -0.4100 -0.7551
#> [ CPUFloatType{2,4} ][ grad_fn = <AddmmBackward0> ]

Note we only use the $train(), since torch modules do not have anything that maps to the state (it is filled by an empty list).

The single hidden layer neural network can be constructed as a Graph, which can then do the training all at once.

po_activation = po("module", id = "activation", activation)
po_module_2 = po("module_2", module = module_2)
po_softmax = po("module", id = "softmax", module = softmax)

module_graph = po_module_1 %>>%
  po_activation %>>%
  po_module_2 %>>%
  po_softmax

module_graph$plot(html = TRUE)

We can now use the graph’s $train() method to pipe a tensor through the whole Graph.

output = module_graph$train(input)[[1]]
output
#> torch_tensor
#>  0.2276  0.3846  0.3878
#>  0.2154  0.3835  0.4011
#> [ CPUFloatType{2,3} ][ grad_fn = <SoftmaxBackward0> ]

While this object allows to easily perform a forward pass, it does not inherit from nn_module, which is useful for various reasons. Instead of having a class that inherits both from nn_module and Graph (which does not work in R6, since multiple inheritance is not available), there is a class that inherits from nn_module and contains a Graph member slot through composition. This class is nn_graph. It is constructed with a Graph, as well as information about the shape(s) of the torch_tensor(s) it expects as inputs.

Shape info is communicated as an integer-valued numeric vector; dimensions that are arbitrary, e.g. batch-size, is given as NA. Our network expects an input of shape c(NA, 3), since the first layer was created as nn_linear(in_features = 3, ...).

If the Graph has multiple outputs, it is also possible to select a subset of outputs to use, or change the output order, by giving the output_map argument.

# the name of the single input is:
module_graph$input
#>              name        train predict    op.id channel.name
#>            <char>       <char>  <char>   <char>       <char>
#> 1: module_1.input torch_tensor    NULL module_1        input

graph_module = nn_graph(
  module_graph,
  shapes_in = list(module_1.input = c(NA, 3))
)

This module gives us the convenience of torch nn_module objects, e.g.:

graph_module$children
#> $module_list
#> An `nn_module` containing 31 parameters.
#> 
#> ── Modules ─────────────────────────────────────────────────────────────────────
#> • 0: <nn_linear> #16 parameters
#> • 1: <nn_sigmoid> #0 parameters
#> • 2: <nn_linear> #15 parameters
#> • 3: <nn_softmax> #0 parameters

And it can be used to transform tensors just as any other torch::nn_module:

graph_module(input)
#> torch_tensor
#>  0.2276  0.3846  0.3878
#>  0.2154  0.3835  0.4011
#> [ CPUFloatType{2,3} ][ grad_fn = <SoftmaxBackward0> ]

Building Torch Models for Tasks using PipeOpTorch

ModelDescriptor

The PipeOpModule represents an nn_module that is fixed for a specific tensor shape and which has no hyperparameters. When constructing a neural network using these operators, one has to take care to have the output shape of operations match the input shapes of the following operations.

A complete Graph of matching PipeOpModules can be constructed using operators that mostly inherit from PipeOpTorch, making use of the ModelDescriptor class. The ModelDescriptor class contains a Graph of (mostly) PipeOpModules and some other information. The PipeOpTorch transforms a ModelDescriptor and adds more PipeOpModules to the Graph.

ModelDescriptors always build up a Graph for a specific Task. The easiest way to initialize a proper ModelDescriptor is to use the appropriate PipeOpTorchIngress for a given datatype. Below we use PipeOpTorchIngressNumeric, which is is is used for numeric data.

task = tsk("iris")$select(colnames(iris)[1:3])

po_torch_in = po("torch_ingress_num")
md = po_torch_in$train(list(task))[[1]]

md
#> <ModelDescriptor: 1 ops>
#> * Ingress:  torch_ingress_num.input: [(NA,3)]
#> * Task:  iris [classif]
#> * Callbacks:  N/A
#> * Optimizer:  N/A
#> * Loss:  N/A
#> * pointer:  torch_ingress_num.output [(NA,3)]

The ModelDescriptor is an S3 object that contains a Graph, information about how to generate data ($ingress and $task), some further tags about how to build a model that are unrelated to architecture ($optimizer, $loss and $callbacks) as well as all further information necessary to extend that graph along a given output ($pointer and $pointer_shape).

unclass(md)
#> $graph
#> Graph with 1 PipeOps:
#>                 ID         State sccssors prdcssors
#>             <char>        <char>   <char>    <char>
#>  torch_ingress_num <<UNTRAINED>>                   
#> 
#> $ingress
#> $ingress$torch_ingress_num.input
#> Ingress: Task[selector_name(c("Petal.Length", "Sepal.Length", "Sepal.Width"), assert_present = TRUE)] --> Tensor(NA, 3)
#> 
#> 
#> $task
#> 
#> ── <TaskClassif> (150x4): Iris Flowers ─────────────────────────────────────────
#> • Target: Species
#> • Target classes: setosa (33%), versicolor (33%), virginica (33%)
#> • Properties: multiclass
#> • Features (3):
#>   • dbl (3): Petal.Length, Sepal.Length, Sepal.Width
#> 
#> $optimizer
#> NULL
#> 
#> $loss
#> NULL
#> 
#> $callbacks
#> named list()
#> 
#> $pointer
#> [1] "torch_ingress_num" "output"           
#> 
#> $pointer_shape
#> [1] NA  3

The $pointer identifies the output of the $graph that PipeOpTorch will extend. Piping this ModelDescriptor through PipeOpTorchLinear, for example, adds a PipeOpModule wrapping a torch::nn_linear.

po_torch_linear = po("nn_linear", out_features = 4)
md = po_torch_linear$train(list(md))[[1]]

md$graph
#> Graph with 2 PipeOps:
#>                 ID         State  sccssors         prdcssors
#>             <char>        <char>    <char>            <char>
#>  torch_ingress_num <<UNTRAINED>> nn_linear                  
#>          nn_linear <<UNTRAINED>>           torch_ingress_num

The $pointer is now updated to identify the output of that PipeOpModule, and the $pointer_shape shows that the shape has changed to 4 units (was 3 for the input before).

md$pointer
#> [1] "nn_linear" "output"
md$pointer_shape
#> [1] NA  4

The model_descriptor_to_module() function converts this to an nn_graph, it is a functional torch::nn_module.

small_module = model_descriptor_to_module(md, list(md$pointer))

small_module(input)
#> torch_tensor
#>  0.2667 -0.0921 -0.5479  1.1549
#>  0.2310  0.6103 -0.2384  0.1594
#> [ CPUFloatType{2,4} ][ grad_fn = <AddmmBackward0> ]

Using ModelDescriptor to get Data

The ModelDescriptor does not only represent the Graph from which a nn_module is created, but also the way in which the Task is is processed to get input batches. A torch::dataset can be created by calling task_dataset(); both the task and the feature_ingress_tokens arguments can be retrieved from the ModelDescriptor. The target_batchgetter needs to be created extra (if necessary), since it depends on the ultimate machine learning model, which we have not looked at so far.

td = task_dataset(
  task = md$task,
  feature_ingress_tokens = md$ingress
)

td
#> <task_dataset>
#>   Inherits from: <dataset>
#>   Public:
#>     .getbatch: function (index) 
#>     .getitem: function (index) 
#>     .length: function () 
#>     all_features: Petal.Length Sepal.Length Sepal.Width Species
#>     cache_lazy_tensors: FALSE
#>     clone: function (deep = FALSE) 
#>     feature_ingress_tokens: list
#>     initialize: function (task, feature_ingress_tokens, target_batchgetter = NULL) 
#>     load_state_dict: function (x, ..., .refer_to_state_dict = FALSE) 
#>     state_dict: function () 
#>     target_batchgetter: NULL
#>     task: TaskClassif, TaskSupervised, Task, R6

Use the $.getbatch() method to get a batch that can be given to the nn_module. Note it has an $x and an $y slot, the latter of which is not used, to account for possible target batches. The $x slot is also a list, since it should be able to handle NNs with multiple inputs (see below).

batch = td$.getbatch(1:3)
batch
#> $x
#> $x$torch_ingress_num.input
#> torch_tensor
#>  1.4000  5.1000  3.5000
#>  1.4000  4.9000  3.0000
#>  1.3000  4.7000  3.2000
#> [ CPUFloatType{3,3} ]
#> 
#> 
#> $.index
#> torch_tensor
#>  1
#>  2
#>  3
#> [ CPULongType{3} ]

small_module(batch$x[[1]])
#> torch_tensor
#> -1.2207  1.8789  0.2275 -0.2343
#> -1.1732  1.9331  0.3023 -0.4274
#> -1.1339  1.7622  0.2150 -0.1968
#> [ CPUFloatType{3,4} ][ grad_fn = <AddmmBackward0> ]

Building sequential NNs

The sequential NN from above can easily be implemented as follows:

graph_generator = po("torch_ingress_num") %>>%
  po("nn_linear", out_features = 4, id = "linear1") %>>%
    po("nn_sigmoid") %>>%
  po("nn_linear", out_features = 3, id = "linear2") %>>%
  po("nn_softmax", dim = 2)

Note how the second nn_linear does not need to be informed about the output dimension of the first nn_linear, since the ModelDescriptor that is passed along the Graph edges knows this info (in the $pointer_shape slot).

md_sequential = graph_generator$train(task)[[1]]

graph_module = model_descriptor_to_module(md_sequential, list(md_sequential$pointer))

graph_module(input)
#> torch_tensor
#>  0.3876  0.1135  0.4989
#>  0.3862  0.1089  0.5049
#> [ CPUFloatType{2,3} ][ grad_fn = <SoftmaxBackward0> ]

Building more interesting NNs

One of the main features of mlr3pipelines is its ability to easily represent computational Graphs. The ModelDescriptor / PipeOpTorch setup is built to make full use of this functionality. It is possible to have multiple inputs into a NN by using multiple PipeOpTorchIngress inputs, it is possible to have parallel and alternative path branching, and it is possible to have multiple outputs.

Consider the following (a bit nonsensical) network that operates differently on the "Petal" than on the "Sepal" features of tsk("iris") We manually split the task here, further down it is shown that the wholly integrated mlr3pipelines pipeline can do this automatically.

iris_petal = tsk("iris")$select(c("Petal.Length", "Petal.Width"))
iris_sepal = tsk("iris")$select(c("Sepal.Length", "Sepal.Width"))
graph_sepal = po("torch_ingress_num", id = "sepal.in") %>>%
  po("nn_linear", out_features = 4, id = "linear1")

graph_petal = po("torch_ingress_num", id = "petal.in") %>>%
  po("nn_linear", out_features = 3, id = "linear2") %>>%
  po("nn_tanh") %>>%
  po("nn_linear", out_features = 5, id = "linear3")

graph_common = ppl("branch", graphs = list(
    sigmoid = po("nn_sigmoid"),
    relu = po("nn_relu")
  )) %>>%
  gunion(list(
    po("nn_linear", out_features = 1, id = "lin_out"),
    po("nn_linear", out_features = 3, id = "cat_out") %>>%
      po("nn_softmax", dim = 2)
  ))


graph_iris = gunion(list(graph_sepal, graph_petal)) %>>%
  po("nn_merge_cat") %>>%
  graph_common

graph_iris$plot(html = TRUE)

We can use this to create a neural network for the iris tasks we created above. We set the $keep_results debug flag here so we can do some inspection about what is happening:

graph_iris$param_set$values$branch.selection = "relu"

graph_iris$keep_results = TRUE

iris_mds = graph_iris$train(
  input = list(sepal.in.input = iris_sepal, petal.in.input = iris_petal),
  single_input = FALSE
)

iris_mds
#> $lin_out.output
#> <ModelDescriptor: 11 ops>
#> * Ingress:  sepal.in.input: [(NA,2)], petal.in.input: [(NA,2)]
#> * Task:  iris [classif]
#> * Callbacks:  N/A
#> * Optimizer:  N/A
#> * Loss:  N/A
#> * pointer:  lin_out.output [(NA,1)]
#> 
#> $nn_softmax.output
#> <ModelDescriptor: 11 ops>
#> * Ingress:  sepal.in.input: [(NA,2)], petal.in.input: [(NA,2)]
#> * Task:  iris [classif]
#> * Callbacks:  N/A
#> * Optimizer:  N/A
#> * Loss:  N/A
#> * pointer:  nn_softmax.output [(NA,3)]

We make multiple observations here:

  1. We can observe how the ModelDescriptor grows as it is passed along the edges of graph_iris. Note that the $graph slot of that ModelDescriptor is often updated by-reference, so by the time we inspect intermediate results, they may contain the complete graph. However, see how the $ingress, $pointer and $pointer_shape of the ModelDescriptors that take the sepal.in-path differ from the ones that take the petal.in-path:

    # sepal.in path
graph_iris$pipeops$linear1$.result[[1]]$ingress
#> $sepal.in.input
#> Ingress: Task[selector_name(c("Sepal.Length", "Sepal.Width"), assert_present = TRUE)] --> Tensor(NA, 2)
graph_iris$pipeops$linear1$.result[[1]]$pointer
#> [1] "linear1" "output"
graph_iris$pipeops$linear1$.result[[1]]$pointer_shape
#> [1] NA  4

# petal.in path
graph_iris$pipeops$linear3$.result[[1]]$ingress
#> $petal.in.input
#> Ingress: Task[selector_name(c("Petal.Length", "Petal.Width"), assert_present = TRUE)] --> Tensor(NA, 2)
graph_iris$pipeops$linear3$.result[[1]]$pointer
#> [1] "linear3" "output"
graph_iris$pipeops$linear3$.result[[1]]$pointer_shape
#> [1] NA  5

    po("nn_merge_cat") unites the two ModelDescriptors and contains the common ingress. The pointer_shape now reflects the output of the “cat”-operation: the 2nd dimension is added up:

    graph_iris$pipeops$nn_merge_cat$.result[[1]]$ingress
#> $sepal.in.input
#> Ingress: Task[selector_name(c("Sepal.Length", "Sepal.Width"), assert_present = TRUE)] --> Tensor(NA, 2)
#> 
#> $petal.in.input
#> Ingress: Task[selector_name(c("Petal.Length", "Petal.Width"), assert_present = TRUE)] --> Tensor(NA, 2)
graph_iris$pipeops$nn_merge_cat$.result[[1]]$pointer_shape
#> [1] NA  9

  2. Multiple ModelDescriptors were created, since the graph_iris has multiple outpus. This makes it possible to create a neural network with multiple outputs. We need to unite the outputs of graph_iris using model_descriptor_union() before we can pass it to model_descriptor_to_module(). We need to collect all output_pointers separately.

    The parameter list_output must be set to TRUE since the module has multiple outputs.

    iris_mds_union = model_descriptor_union(iris_mds[[1]], iris_mds[[2]])
output_pointers = list(iris_mds[[1]]$pointer, iris_mds[[2]]$pointer)
output_pointers
#> [[1]]
#> [1] "lin_out" "output" 
#> 
#> [[2]]
#> [1] "nn_softmax" "output"
iris_module = model_descriptor_to_module(iris_mds_union, output_pointers, list_output = TRUE)

  3. The PipeOpBranch disappears in the resulting Graph of PipeOpModule in the iris_module. This is because only the PipeOpTorchs in the graph_iris add anything to the ModelDescriptors. The branch is interpeted when graph_iris runs, and only the nn_relu path is followed. The iris_module therefore contains a Graph that does “relu” activation:

    iris_module$graph$plot(html = TRUE)

  4. The ModelDescriptor’s $task slot contains a Task with all features that are used to create the input data for all NN inputs. It can be given to task_dataset(), along with the $ingress, to create a torch dataset that creates all batches. As above, any output of graph_iris can be used:

    iris_mds_union$task  # contains all features
#> 
#> ── <TaskClassif> (150x5): Iris Flowers ─────────────────────────────────────────
#> • Target: Species
#> • Target classes: setosa (33%), versicolor (33%), virginica (33%)
#> • Properties: multiclass
#> • Features (4):
#>   • dbl (4): Petal.Length, Petal.Width, Sepal.Length, Sepal.Width

iris_td = task_dataset(
  task = iris_mds_union$task,
  feature_ingress_tokens = iris_mds_union$ingress
)

batch = iris_td$.getbatch(1:2)
batch
#> $x
#> $x$sepal.in.input
#> torch_tensor
#>  5.1000  3.5000
#>  4.9000  3.0000
#> [ CPUFloatType{2,2} ]
#> 
#> $x$petal.in.input
#> torch_tensor
#>  1.4000  0.2000
#>  1.4000  0.2000
#> [ CPUFloatType{2,2} ]
#> 
#> 
#> $.index
#> torch_tensor
#>  1
#>  2
#> [ CPULongType{2} ]

  5. The resulting module has multiple inputs and multiple outputs. We call it with the first two rows of iris, but set the debug $keep_results flag so we can inspect what is happening in the nn_module’s $graph:

    iris_module$graph$keep_results = TRUE

iris_module(
  sepal.in.input = batch$x$sepal.in.input,
  petal.in.input = batch$x$petal.in.input
)
#> $lin_out.output
#> torch_tensor
#>  0.2105
#>  0.1664
#> [ CPUFloatType{2,1} ][ grad_fn = <AddmmBackward0> ]
#> 
#> $nn_softmax.output
#> torch_tensor
#>  0.2850  0.2173  0.4977
#>  0.2879  0.2353  0.4768
#> [ CPUFloatType{2,3} ][ grad_fn = <SoftmaxBackward0> ]

    The first linear layer that takes “Sepal” input ("linear1") creates a 2x4 tensor (batch size 2, 4 units), while the "linear3" layer has 2x5 output:

    iris_module$graph$pipeops$linear1$.result
#> $output
#> torch_tensor
#>  1.7258  1.4360 -0.9824 -2.1879
#>  1.4928  1.2838 -0.8334 -1.9567
#> [ CPUFloatType{2,4} ][ grad_fn = <AddmmBackward0> ]
iris_module$graph$pipeops$linear3$.result
#> $output
#> torch_tensor
#> -0.1228 -0.0173 -0.2099 -0.6401 -0.3833
#> -0.1228 -0.0173 -0.2099 -0.6401 -0.3833
#> [ CPUFloatType{2,5} ][ grad_fn = <AddmmBackward0> ]

    We observe that the po("nn_merge_cat") concatenates these, as expected:

    iris_module$graph$pipeops$nn_merge_cat$.result
#> $output
#> torch_tensor
#>  1.7258  1.4360 -0.9824 -2.1879 -0.1228 -0.0173 -0.2099 -0.6401 -0.3833
#>  1.4928  1.2838 -0.8334 -1.9567 -0.1228 -0.0173 -0.2099 -0.6401 -0.3833
#> [ CPUFloatType{2,9} ][ grad_fn = <CatBackward0> ]

Building Torch Learners

We have now seen how NN Graphs of PipeOpModule are created and turned into nn_modules. Using PipeOpTorch even creates ModelDescriptor objects that contain additional info about how batch tensors are extracted from Tasks. For a complete Learner, it is still necessary to define the loss-function used for optimization, the optimizer, and optionally some callbacks. We have already covered their class representations – TorchLoss, TorchOptimizer, TorchCallbacks, in the Get Started vignette. Here we use adam as the optimizer, cross-entropy as the loss function, and the history callback.

adam = t_opt("adam", lr = 0.02)
adam
#> <TorchOptimizer:adam> Adaptive Moment Estimation
#> * Generator: optim_ignite_adam
#> * Parameters: lr=0.02
#> * Packages: torch,mlr3torch

xe = t_loss("cross_entropy")
xe
#> <TorchLoss:cross_entropy> Cross Entropy
#> * Generator: function
#> * Parameters: list()
#> * Packages: torch,mlr3torch
#> * Task Types: classif

history = t_clbk("history")
history
#> <TorchCallback:history> History
#> * Generator: CallbackSetHistory
#> * Parameters: list()
#> * Packages: mlr3torch,torch

LearnerTorchModel

LearnerTorchModel represents a supervised model (regression or classification) using torch NNs. It needs a nn_module, as well as a list of TorchIngressToken that define how batches are created from a Task. TorchIngressToken hard-code the column-names of a Task that are used for data-input, the Learner created like this therefore only works for the specific Task created. (Generally the full mlr3pipelines-UI should be used if this is a problem, see below.) The following uses the sequential NN from above:

lr_sequential = lrn("classif.torch_model",
  task_type = "classif",
  network = model_descriptor_to_module(md_sequential, list(md_sequential$pointer)),
  ingress_tokens = md_sequential$ingress,
  optimizer = adam,
  callbacks = history,
  loss = xe
)

lr_sequential
#> 
#> ── <LearnerTorchModel> (classif.model): Torch Model ────────────────────────────
#> • Model: -
#> • Parameters: device=auto, num_threads=1, num_interop_threads=1, seed=random,
#> eval_freq=1, measures_train=<list>, measures_valid=<list>, patience=0,
#> min_delta=0, shuffle=TRUE, tensor_dataset=FALSE, jit_trace=FALSE, opt.lr=0.02
#> • Validate: NULL
#> • Packages: mlr3, mlr3torch, and torch
#> • Predict Types: [response] and prob
#> • Feature Types: logical, integer, numeric, character, factor, ordered,
#> POSIXct, Date, and lazy_tensor
#> • Encapsulation: none (fallback: -)
#> • Properties: featureless, hotstart_backward, hotstart_forward, importance,
#> internal_tuning, marshal, missings, multiclass, offset, oob_error,
#> selected_features, twoclass, validation, and weights
#> • Other settings: use_weights = 'use'
#> • Optimizer: adam
#> • Loss: cross_entropy
#> • Callbacks: history

Before training the model, we set some more hyperparameters.

lr_sequential$param_set$set_values(
  batch_size = 50,
  epochs = 100,
  measures_train = msrs(c("classif.logloss", "classif.ce"))
)
# This is required to evaluate the logloss during training
lr_sequential$predict_type = "prob"

lr_sequential$train(md_sequential$task)

The following calls the $predict_newdata function to plot the response surface along the Sepal.Width = mean(Sepal.Width) plane, along with the ground-truth values:

library(data.table)
library(ggplot2)

newdata = cbind(data.table(Sepal.Width = mean(iris$Sepal.Width)), CJ(
  Sepal.Length = seq(min(iris$Sepal.Length), max(iris$Sepal.Length), length.out = 30),
  Petal.Length = seq(min(iris$Petal.Length), max(iris$Petal.Length), length.out = 30)
))

predictions = lr_sequential$predict_newdata(newdata)

plot_predictions = function(predictions) {
  ggplot(cbind(newdata, Species = predictions$response),
      aes(x = Sepal.Length, y = Petal.Length, fill = Species)) +
    geom_tile(alpha = .3) +
    geom_tile(alpha = .3) +
    geom_point(data = iris,
      aes(x = Sepal.Length, y = Petal.Length, fill = Species),
      color = "black", pch = 21, size = 3) +
    theme_bw()
}
plot_predictions(predictions)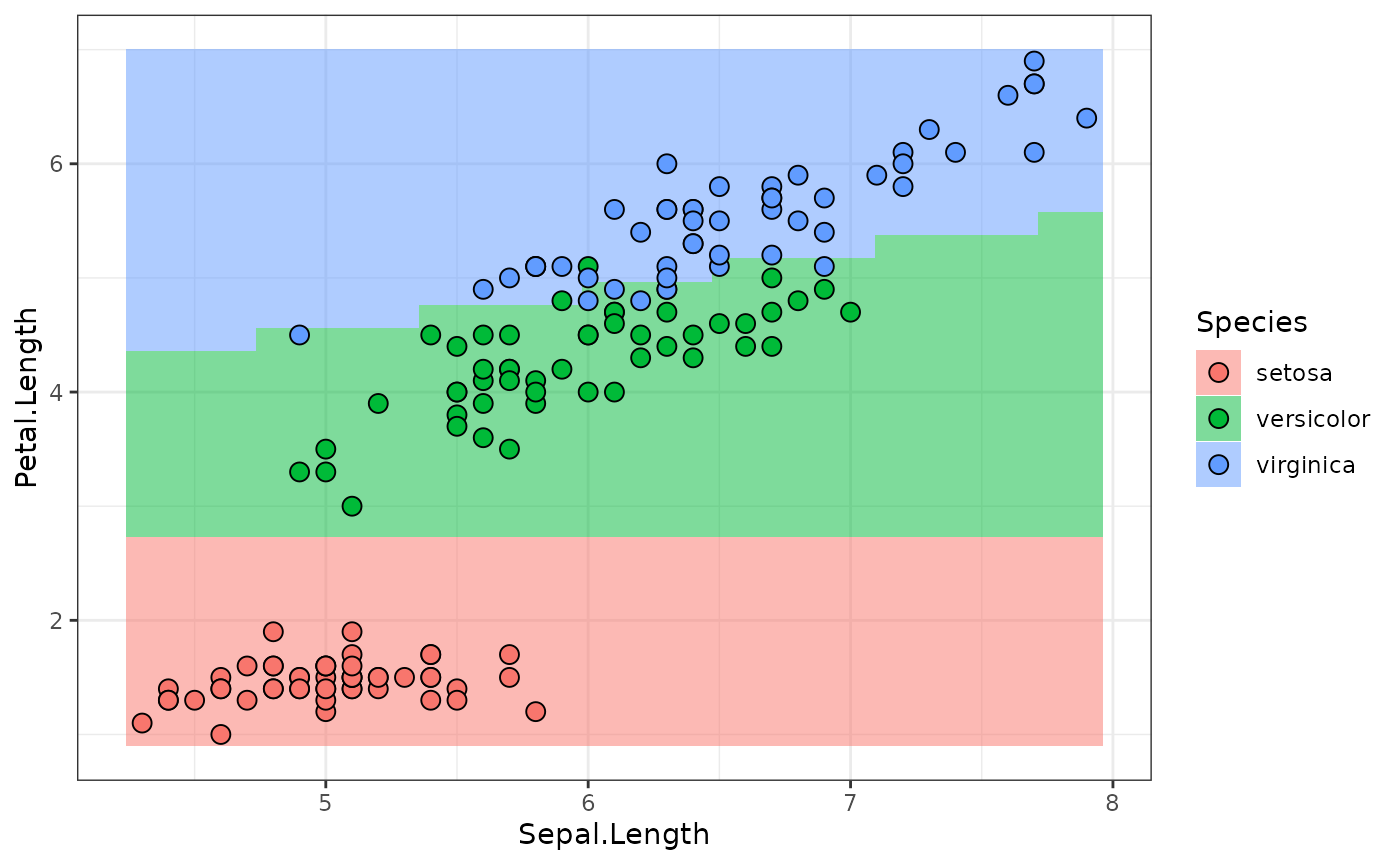

Torch Learner Pipelines

The model shown above is constructed using the ModelDescriptor that is generated from a Graph of PipeOpTorch operators. The ModelDescriptor furthermore contains the Task to which it pertains. This makes it possible to use it to create a NN model that gets trained right away, using PipeOpTorchModelClassif. The only missing prerequisite now is to add the desired TorchOptimizer and TorchLoss information to the ModelDescriptor.

Adding Optimizer, Loss and Callback Meta-Info to ModelDescriptor

Remember that ModelDescriptor has the $optimizer, $loss and $callbacks slots that are necessary to build a complete Learner from an NN. They can be set by corresponding PipeOpTorch operators.

po("torch_optimizer") is used to set the $optimizer slot of a ModelDescriptor; it takes the desired TorchOptimizer object on construction and exports its ParamSet.

po_adam = po("torch_optimizer", optimizer = adam)

# hyperparameters are made available and can be changed:
po_adam$param_set$values
#> $lr
#> [1] 0.02

md_sequential = po_adam$train(list(md_sequential))[[1]]

md_sequential$optimizer
#> <TorchOptimizer:adam> Adaptive Moment Estimation
#> * Generator: optim_ignite_adam
#> * Parameters: lr=0.02
#> * Packages: torch,mlr3torch

This works analogously for the loss-function.

po_xe = po("torch_loss", loss = xe)
md_sequential = po_xe$train(list(md_sequential))[[1]]

md_sequential$loss
#> <TorchLoss:cross_entropy> Cross Entropy
#> * Generator: function
#> * Parameters: list()
#> * Packages: torch,mlr3torch
#> * Task Types: classif

And also for callbacks:

po_history = po("torch_callbacks", callbacks = t_clbk("history"))
md_sequential = po_history$train(list(md_sequential))[[1]]

md_sequential$callbacks
#> $history
#> <TorchCallback:history> History
#> * Generator: CallbackSetHistory
#> * Parameters: list()
#> * Packages: mlr3torch,torch

Combined Instantiation and Training of LearnerTorchModel

The ModelDescriptor can now be given to a po("torch_model_classif").

po_model = po("torch_model_classif", batch_size = 50, epochs = 50)

po_model$train(list(md_sequential))
#> $output
#> NULL

po("torch_model_classif") behaves similarly to a PipeOpLearner: It returns NULL during training, and the prediction on $predict(). po("torch_model_classif") behaves similarly to a PipeOpLearner: It returns NULL during training, and the prediction on $predict().

newtask = TaskClassif$new("newdata", cbind(newdata, Species = factor(NA, levels = levels(iris$Species))), target = "Species")

predictions = po_model$predict(list(newtask))[[1]]

plot_predictions(predictions)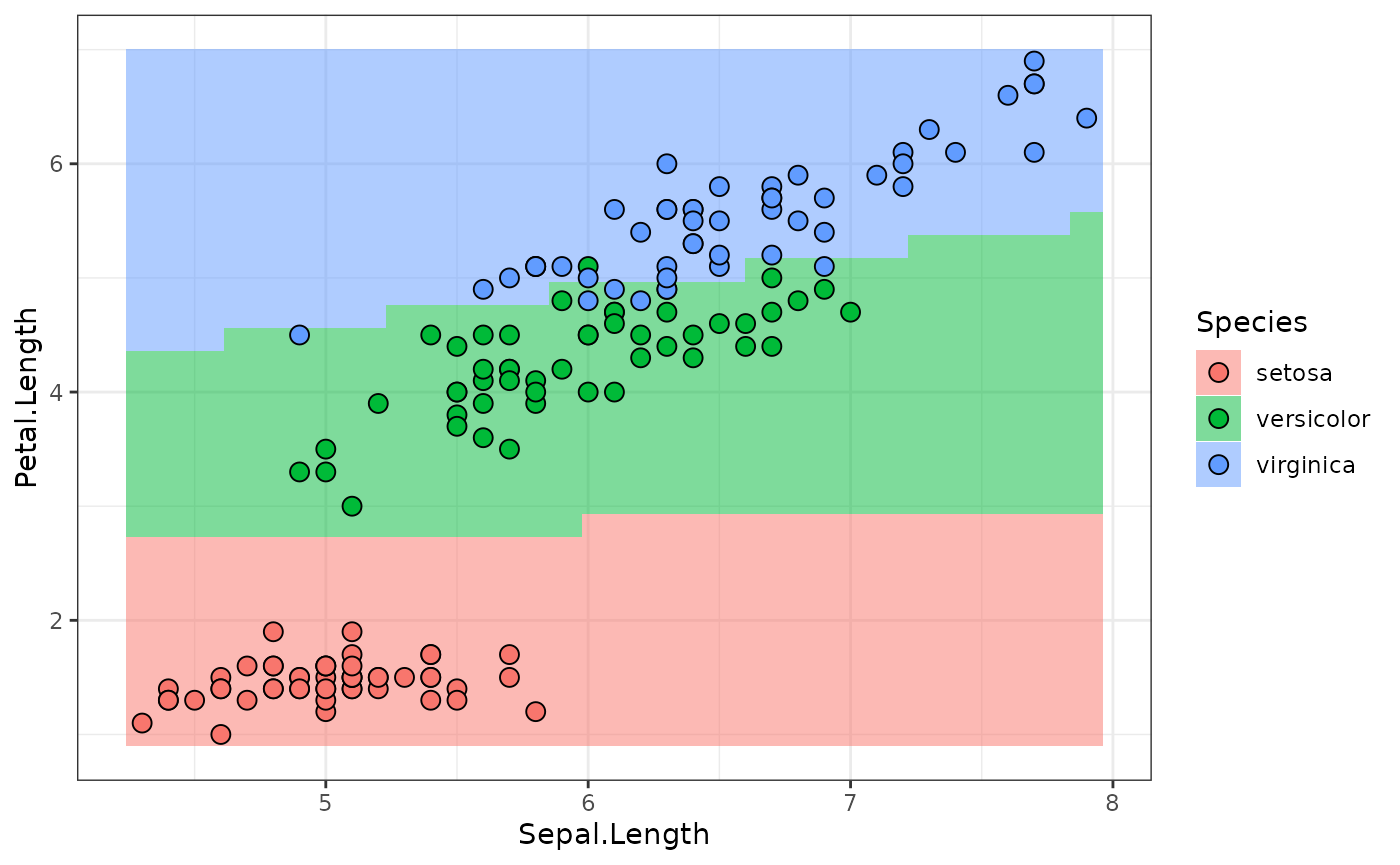

The whole Pipeline

Remember that md_sequential was created using a Graph that the initial Task was piped through. If we combine such a Graph with PipeOpTorchModelClassif, we get a Graph that behaves like any other Graph that ends with a PipeOpLearner, and can therefore be wrapped as a GraphLearner. The following uses one more hidden layer than before:

graph_sequential_full = po("torch_ingress_num") %>>%
  po("nn_linear", out_features = 4, id = "linear1") %>>%
    po("nn_sigmoid") %>>%
    po("nn_linear", out_features = 3, id = "linear2") %>>%
    po("nn_softmax", dim = 2, id = "softmax") %>>%
    po("nn_linear", out_features = 3, id = "linear3") %>>%
    po("nn_softmax", dim = 2, id = "softmax2") %>>%
    po("torch_optimizer", optimizer = adam) %>>%
    po("torch_loss", loss = xe) %>>%
    po("torch_callbacks", callbacks = history) %>>%
    po("torch_model_classif", batch_size = 50, epochs = 100)
lr_sequential_full = as_learner(graph_sequential_full)

lr_sequential_full$train(task)

Compare the resulting Graph

graph_sequential_full$plot(html = TRUE)

With the Graph of the trained model:

model = lr_sequential_full$graph_model$state$torch_model_classif$model
model$network$graph$plot(html = TRUE)

Predictions, as before (we can use predict_newdata again):

predictions = lr_sequential_full$predict_newdata(newdata)

plot_predictions(predictions)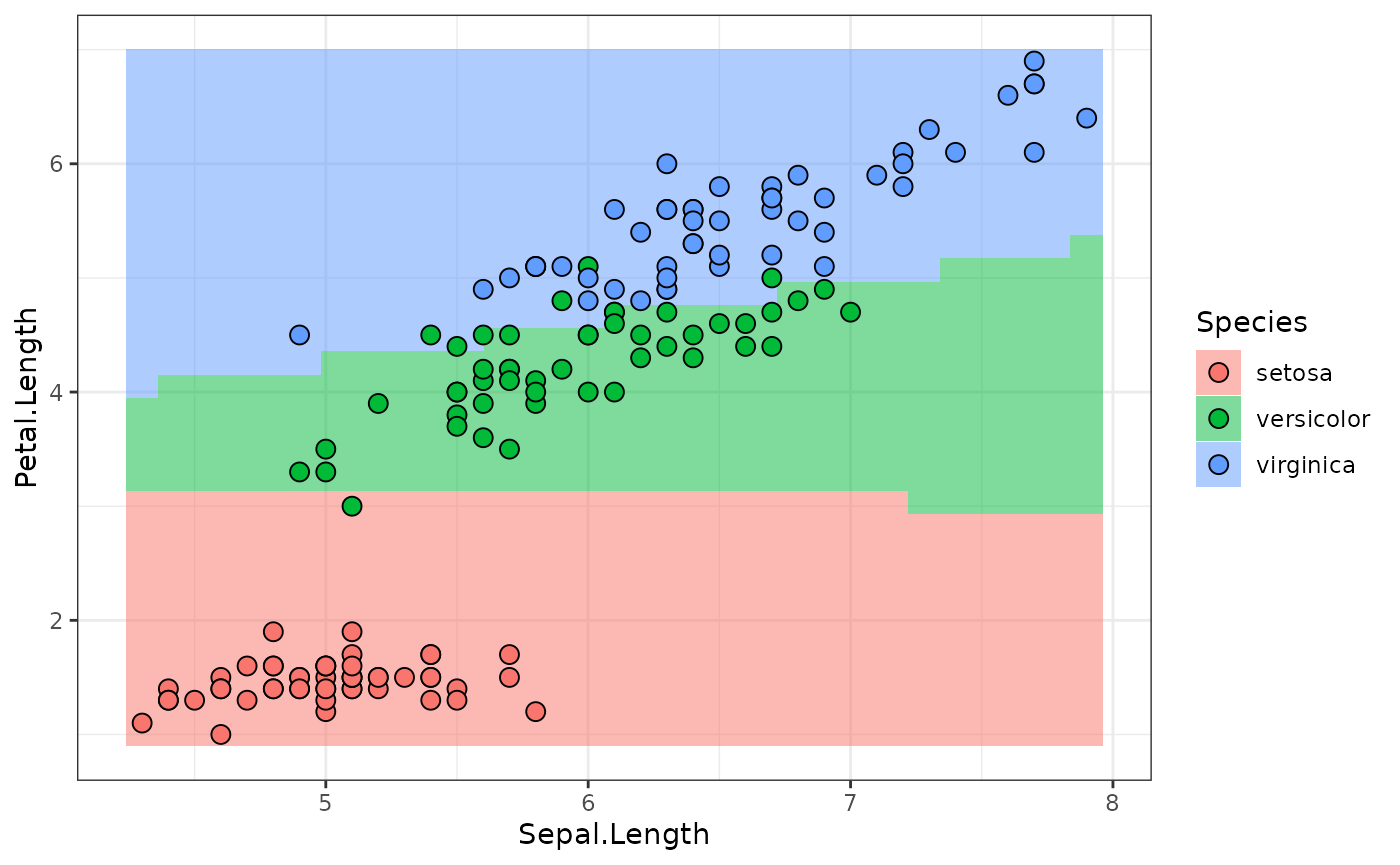

Mixed Pipelines

We are not just limited to PipeOpTorch in these kinds of Graphs, and we are also not limited to having only a single PipeOpTorchIngress. The following pipeline, for example, removes all but the Petal.Length columns from the Task and fits a model:

gr = po("select", selector = selector_name("Petal.Length")) %>>%
  po("torch_ingress_num") %>>%
  po("nn_linear", out_features = 5, id = "linear1") %>>%
  po("nn_relu") %>>%
  po("nn_linear", out_features = 3, id = "linear2") %>>%
  po("nn_softmax", dim = 2) %>>%
  po("torch_optimizer", optimizer = adam) %>>%
  po("torch_loss", loss = xe) %>>%
  po("torch_model_classif", batch_size = 50, epochs = 50)

gr$plot(html = TRUE)
lr = as_learner(gr)
lr$train(task)
predictions = lr$predict_newdata(newdata)

plot_predictions(predictions)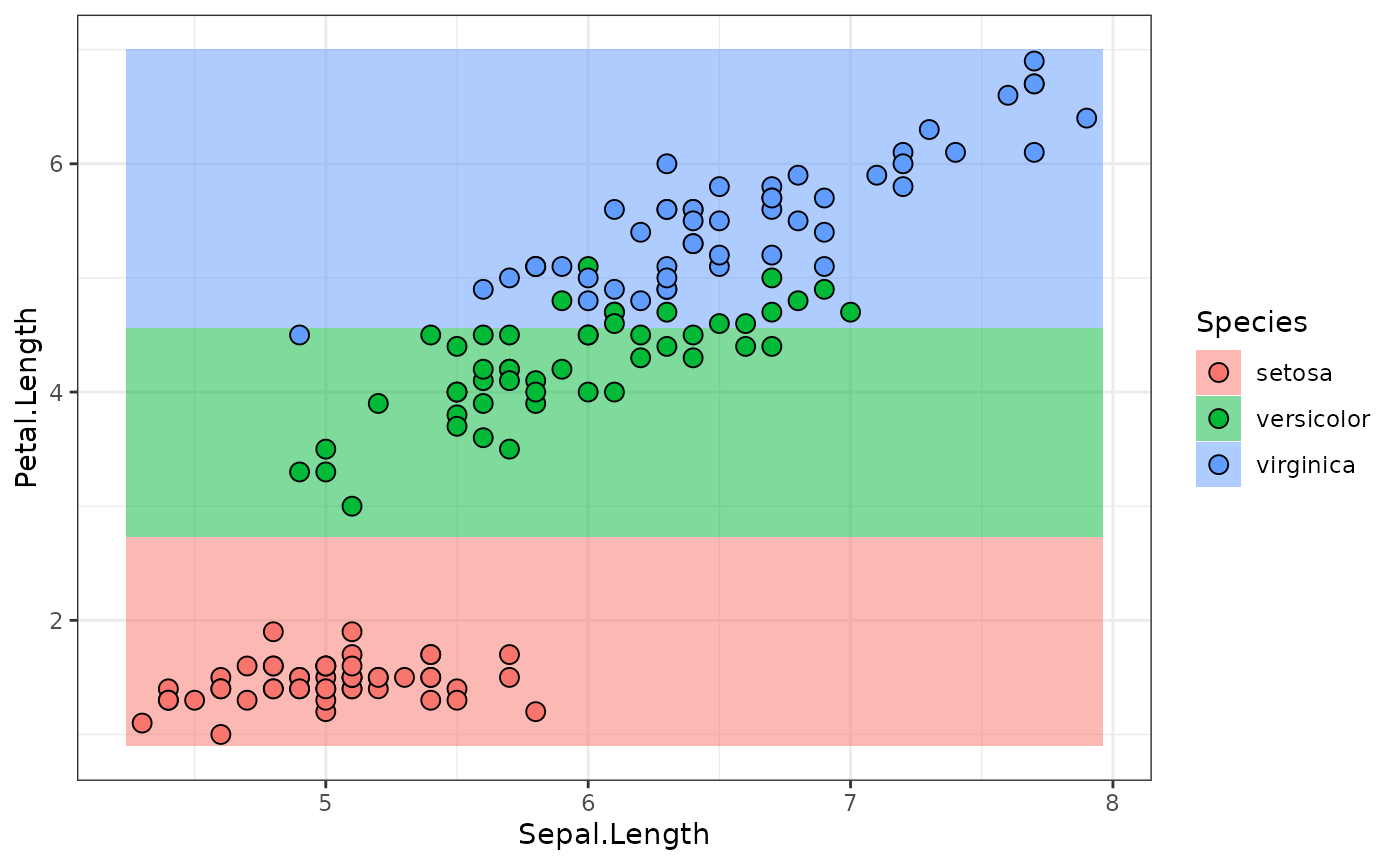

How about using Petal.Length and Sepal.Length separately at first?

gr = gunion(list(
      po("select", selector = selector_name("Petal.Length"), id = "sel1") %>>%
        po("torch_ingress_num", id = "ingress.petal") %>>%
        po("nn_linear", out_features = 3, id = "linear1"),
      po("select", selector = selector_name("Sepal.Length"), id = "sel2") %>>%
        po("torch_ingress_num", id = "ingress.sepal") %>>%
        po("nn_linear", out_features = 3, id = "linear2")
    )) %>>%
    po("nn_merge_cat")  %>>%
    po("nn_relu", id = "act1") %>>%
    po("nn_linear", out_features = 3, id = "linear3") %>>%
    po("nn_softmax", dim = 2, id = "act3") %>>%
    po("torch_optimizer", optimizer = adam, lr = 0.1) %>>%
    po("torch_loss", loss = xe) %>>%
    po("torch_model_classif", batch_size = 50, epochs = 50)

gr$plot(html = TRUE)
lr = as_learner(gr)
lr$train(task)
predictions = lr$predict_newdata(newdata)

plot_predictions(predictions)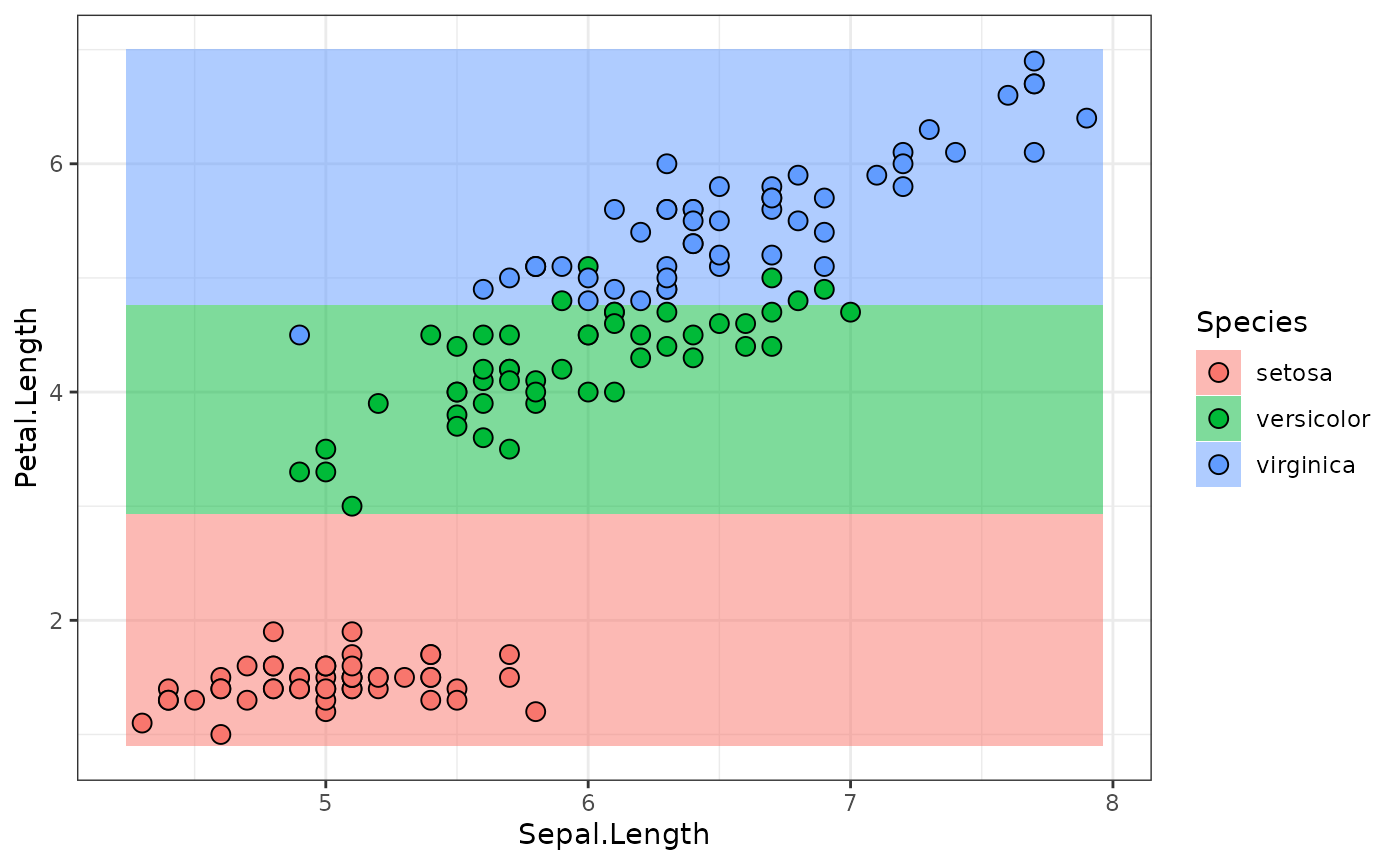

All these examples have hopefully demonstrated the possibilities that come with the representation of neural network layers as PipeOps. Even though this vignette was quite technical, we hope to have given you an in-depth understanding of the underlying mechanisms.